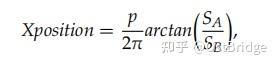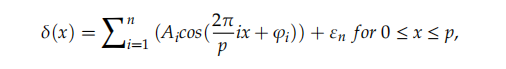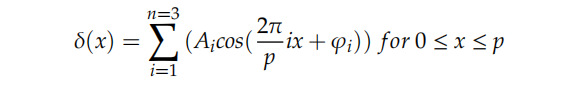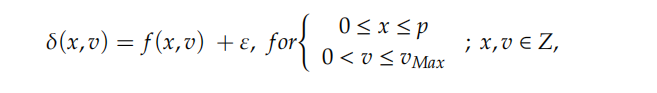1. Einführung in den Encoder
Optische Encoder gelten als die zuverlässigsten Geräte für präzise Messungen und Bewegungssteuerung. Dank ihrer hohen Genauigkeit, Auflösung und Wiederholgenauigkeit sowie ihrer Einsatzfähigkeit unter verschiedenen Umgebungsbedingungen und ihres vergleichsweise niedrigen Preises finden sie in vielfältigen Anwendungen Verwendung. Beispiele hierfür sind handgeführte Werkzeugmaschinen und CNC-Werkzeugmaschinen, Roboter, Servicesysteme, Überwachungs- und Fehlerdiagnosesysteme, Trackingsysteme, Linear- und Drehtische sowie weitere Präzisionspositionierungsanwendungen.
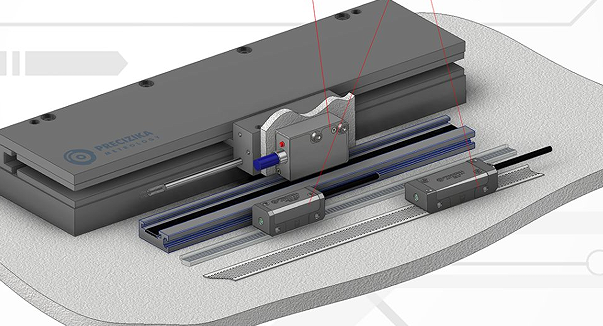
Die Gesamtgenauigkeit und Präzision eines
Linearencoder Die Genauigkeit hängt hauptsächlich von der Qualität der Messskala und dem nichtlinearen Unterteilungsfehler (SDE) innerhalb eines Signalzyklus ab. Hohe Genauigkeit und Auflösung sind entscheidend für Anwendungen, die präzise Positionierung und gute Wiederholgenauigkeit erfordern. In manchen Anwendungen dienen elektronische Encoder nicht nur der Positionsbestimmung, sondern liefern auch Rückmeldung für die Drehzahlregelung.
SDE (auch bekannt als Interpolationsfehler) ist ein Zyklus, der während jeder Periode auftritt " target="_blank" rel="noopener">DrehgeberrotationAbhängig von der Qualität der Hauptmessskala des erzeugten elektrischen Signals entsteht dieser Fehler während der Interpolation, da das verzerrte analoge elektronische Signal des Encoders die Bildung eines neuen Vierecksignals verhindert. In der Praxis verursacht der SDE (Standardized Differential Error) erst dann Probleme, wenn seine Amplitude die Größe des Messschritts erreicht. Anders ausgedrückt: Die Größe des SDE begrenzt die höchste Auflösung. Bei einem großen Positionierfehler ist der kleinste messbare Inkrementschritt bedeutungslos. Dies ist besonders wichtig für Anwendungen, die präzise Positionierung und Wiederholgenauigkeit erfordern. In Maschinen mit direkt angetriebener Vorschubachse oder direkt angetriebenem Drehtisch verursachen nichtlineare Interpolationsfehler nicht nur Positionierfehler, sondern auch laute Geräusche, zusätzliche Erwärmung und Drehzahlreduzierung.
Die Qualität eines elektrischen Signals hängt maßgeblich von verschiedenen Aspekten ab, wie dem optischen Abtastprinzip, der Konstruktion des Lesekopfes und seiner Beständigkeit gegenüber Verformungen, mechanischen Vibrationen und Temperaturschwankungen. Um die Signalqualität zu verbessern und den Encoder robuster zu gestalten, setzen Hersteller fortschrittliche optische Abtastverfahren wie Einzelfeld- oder interferometrische Abtastverfahren ein oder verwenden speziell konfigurierte Mehrspur-Analysatorgitter zur Eliminierung von Oberwellen. Leider erfordern all diese Verbesserungen komplexere Encoderkonfigurationen und teurere optische Komponenten. Nicht-äquivalente Signalparameter wie relative Amplitude, DCo-Einstellung, Phasenverschiebung und nicht-sinusförmige Wellenform müssen vor der Interpolation korrigiert werden. Viele Forschungsmethoden zur Lösung dieses Problems beinhalten die Verwendung digitaler Korrektur- und Prospekttabellen oder die Entwicklung verschiedener Algorithmen zur Linien- und Dynamikkompensation. Aufgrund des geringen Bereichs von SDE, die Wiederholungen in jedem Zyklus aufweisen, ist ihre Kompensation eine schwierige Aufgabe.
Es ist entscheidend, die Funktionsgrenzen des verwendeten Wegmessgebers zu verstehen, um einen reibungslosen Betrieb der Anwendung und die Durchführung geeigneter Anpassungen zu gewährleisten. Der spezifische Differenzialfehler (SDE) ist einer der Parameter, der zuerst untersucht werden sollte, insbesondere wenn das elektrische Signal des Gebers vor der Interpolation nicht korrigiert oder kompensiert wird. Die in diesem Artikel vorgestellte Methode ermöglicht die Abschätzung der Größe des Interpolationsfehlers und seines zeitlichen Verlaufs. Experimentelle Untersuchungen zu Interpolationsfehlern spezifischer Standardgeber bei unterschiedlichen Abtastgeschwindigkeiten haben gezeigt, dass die Größe dieses niederfrequenten Fehlers maßgeblich von der Verfahrgeschwindigkeit des Lesekopfes abhängt. Darüber hinaus kann eine detaillierte harmonische Analyse des SDE ein besseres Verständnis der physikalischen Eigenschaften der Fehler ermöglichen und die Leistung der Geber sowie der gesamten Anwendung verbessern.
2. Der Messprozess und der Unterteilungsfehler optischer Encoder
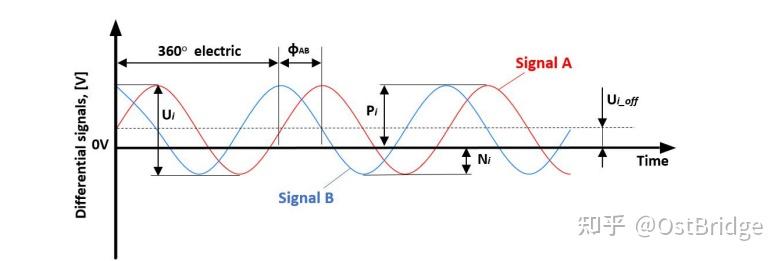
Verschiedene optische Abtastprinzipien für Fotodioden (wie Talbot-Effekt, Lau-Effekt, Moiré-Effekt, verallgemeinerte Gitterabbildung und Interferometrie) werden genutzt, um elektronische Ausgangssignale zur präzisen Positionsbestimmung zu erzeugen. Abhängig von den verwendeten elektronischen Bauelementen können optische Encoder unterschiedliche Schnittstellen aufweisen, um einen zuverlässigen Informationsaustausch zu gewährleisten. Eine der am häufigsten verwendeten Schnittstellen für die inkrementelle Positionsmessung besteht aus zwei analogen, nahezu sinusförmigen Spannungssignalen (Abbildung 1). Die Signale A und B sind um 90 Grad phasenverschoben und weisen typischerweise eine Amplitude von 1 Vpp auf.
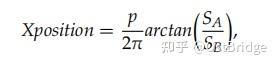
Dabei bezeichnet Xposition die relative Position zwischen der Messskala und dem Lesekopf; p die Periode des Hauptlineals; SA, SB die Perioden der Werte der Ausgangssignale A und B an einer bestimmten Position; SA und SB sind die Werte der Ausgangssignale A und B an einer bestimmten Position.
Abbildung 1. Definition des differentiellen optischen Encodersignals (1 Vpp)
Dieser Prozess wird als Interpolation bezeichnet und steht in direktem Zusammenhang mit der Signalqualität. Die 1-Vpp-Schnittstelle wird hauptsächlich in Anwendungen eingesetzt, in denen Interpolation und Digitalisierung analoger Signale von nachfolgenden elektronischen Geräten in Endgeräten durchgeführt werden.
Die Qualität und Genauigkeit des Encoders lassen sich bequem beobachten und verfolgen, indem man das simulierte Encodersignal auf der X- und Y-Achse des Oszilloskops darstellt. In der Praxis wird das Encodersignal jedoch durch Fertigungs-, Montage- und optische Abtastfehler sowie durch Umwelteinflüsse verzerrt. Diese Signalverzerrung führt zu einem Signal-Dispersions-Effekt (SDE), der sich in jedem Zyklus des Encodergitters wiederholt. Die Änderung des Signalhintergrundpegels (UA_o_off, UB_o_off) wird üblicherweise durch Defekte oder Verunreinigungen auf der Messskala des Encoders verursacht. Diese Verzerrung führt zu einer Abweichung um die Lissajous-Kurve (siehe Abbildung 2a). Die inkonsistente Amplitude (UA, UB) zwischen den Signalspitzen A und B kann auf eine ungleichmäßige oder inkonsistente Ausleuchtung des Fotodetektors zurückzuführen sein. Abbildung 2c zeigt, dass eine Phasenverschiebung von 90° eine Änderung der Kurve bewirkt. Hauptursache für diesen Fehler ist die Neigung zwischen der Abdeckung des Abtastgitters und der Hauptmessskala. Alle durch Optoelektronik und Elektronik verursachten höheren Harmonischen führen dazu, dass das Signal keine perfekte Sinuswelle mehr ist. Dieser Fehler erzeugt eine nicht-kreisförmige Lissajous-Kurve, wie in Abbildung 2d dargestellt.
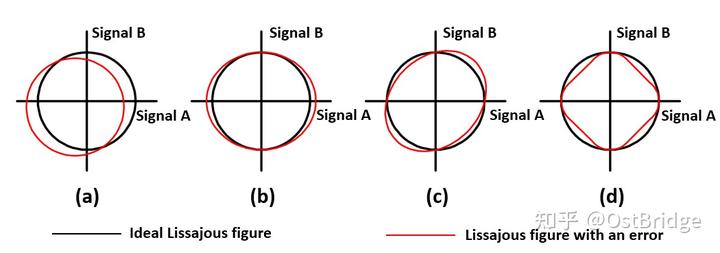
Abbildung 2. Lissajous-Kurve des optischen Encodersignals mit relativem Unterteilungsfehler (SDE): (a) Einstellfehler; (b) Amplitudenfehler; (c) Phasenschieberfehler; (d) Signalformfehler.
3. Erhebungsmethoden und experimentelle Rahmenbedingungen
Die magnetische Kraft des Normalform-SDE wird üblicherweise mithilfe eines Referenzencoders und eines Laserinterferometers bestimmt. Die Differenz zwischen den unabhängigen Positionsinformationen des Referenzgeräts und dem letzten Messwert des Linearencoders gilt als Fehler.
Eine weitere in dieser Arbeit angewandte Methode basiert auf der Messung mit konstanter Geschwindigkeit. Der zu testende Encoder-Lesekopf wird mit konstanter Geschwindigkeit angesteuert und sein Ausgangssignal mit einem digitalen Oszilloskop aufgezeichnet. Aufgrund der hohen Abtastfrequenz wird das Signal des Analog-Encoders als eine Menge diskreter Punkte dargestellt. Unter der Annahme einer konstanten Abtastgeschwindigkeit und der Berücksichtigung der Nyquist-Shannon-Abtastung bei der Anzahl der verwendeten Abtastwerte bedeutet dies, dass an diesen Punkten theoretisch plausible Positionswerte kombiniert werden. Beträgt die Abtastgeschwindigkeit beispielsweise 100 mm/s, die Gitterperiode des Test-Encoders 20 µm und die Abtastfrequenz 250 MHz, so ergeben sich 50000 Abtastpunkte pro Zyklus. Der erste Punkt entspricht dem Positionswert des Lasers, der letzte Punkt (50000) entspricht 20 µm. Um statistisch zuverlässige Ergebnisse zu erhalten, muss dieses Programm mehrere Zyklen und verschiedene Messwerte wiederholen und die Mittelwertbildung angewendet werden.
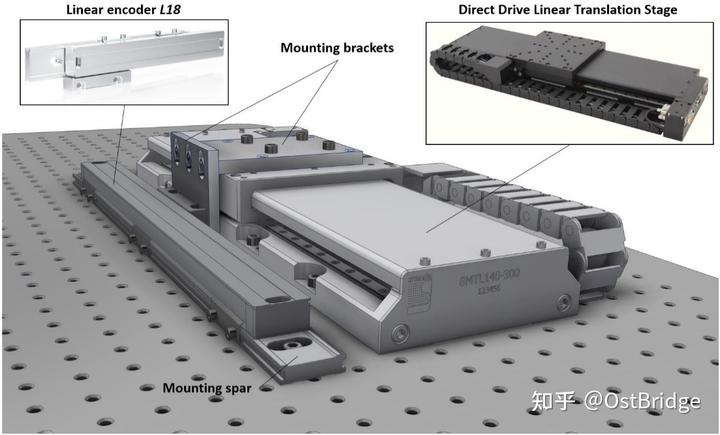
Als experimentelles Forschungsobjekt wählten wir einen Standard-Optik-Encoder (4-Feld-Abtastung). Eine mobile Übersetzungsplattform auf Basis von Direktantriebstechnologie dient dazu, die hohe Genauigkeit und geringe Reibung des Lesekopfes des Encoders bei verschiedenen konstanten Geschwindigkeiten zu testen.
Abbildung 3. Versuchsaufbau. Der Testleitungs-Encoder ist über eine Montagehalterung mit der Übersetzungsstrebe der Direktantriebsleitung verbunden.
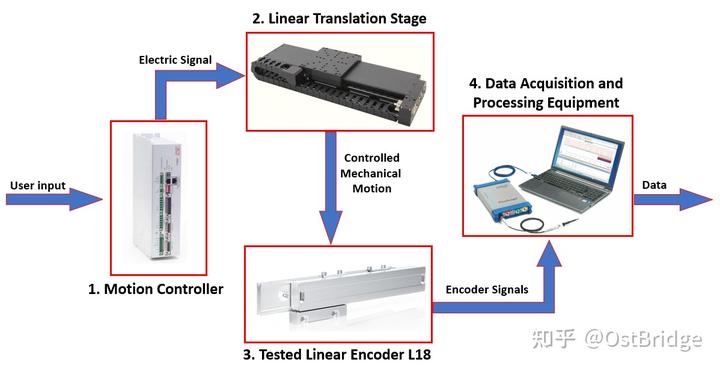
Der dreiphasige Drahtbürsten-Servomotor im Translationstisch wird von einem ACS-Servo-Bewegungsregler mit integriertem Treiber gesteuert. In der Translationsphase dient ein integrierter, berührungsloser linearer optischer Encoder als Rückkopplungssystem für hochauflösende Positionierung und gleichmäßige Bewegungssteuerung. Elektrische Signale werden mit einem digitalen Oszilloskop abgetastet und aufgezeichnet. Das Schaltbild des Versuchsaufbaus ist in Abbildung 4 dargestellt.
Abbildung 4. Schematische Darstellung des Versuchsaufbaus
Der Versuchsaufbau umfasst:
1. Bewegungssteuerung: Servo-Bewegungssteuerung mit eingebautem Treiber ACS-Bewegungssteuerung SPiiPlusCMnt.
2. Lineare Translationsplattform: Elektrische, direkt angetriebene lineare Translationsplattform "STANDA" 8MTL1401-300.
3. Getesteter Linear-Encoder: Optischer Linear-Encoder PrecizikaMetrologyL18 (4-Gitter-Scanning) (Messlänge = 300 mm, Gitterperiode = 20 µ m).
4. Datenerfassungs- und -verarbeitungsausrüstung: ein digitales Oszilloskop PicoScope3000 und ein Laptop mit entsprechender Software.
Um die Eigenschaften dieser Fehler bei verschiedenen Geschwindigkeiten zu analysieren, wurde der Algorithmus der schnellen Fourier-Transformation (FFT) verwendet. Da diese Fehler zyklisch auftreten, hilft ihre harmonische Analyse, neue Signalfehler zu identifizieren, die diese Fehler verursachen. Harmonische dritter und höherer Ordnung entstehen durch Verzerrungen elektrischer Signale höherer Ordnung. Üblicherweise werden sie durch den Doppelbrechungseffekt während des optischen Modulationsprozesses verursacht. Daher kann der aus Harmonischen zusammengesetzte Fehler durch die folgende Formel dargestellt werden:
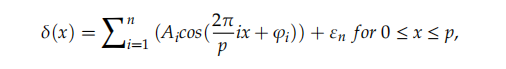
unter δ (x) Repräsentiert die SDE des Encodergitters innerhalb eines Zyklus, Ai und ji repräsentieren die Amplitude und Phase der Harmonischen, und x repräsentiert die relative Position innerhalb eines Zyklus p.
4. Resultate und Diskussion
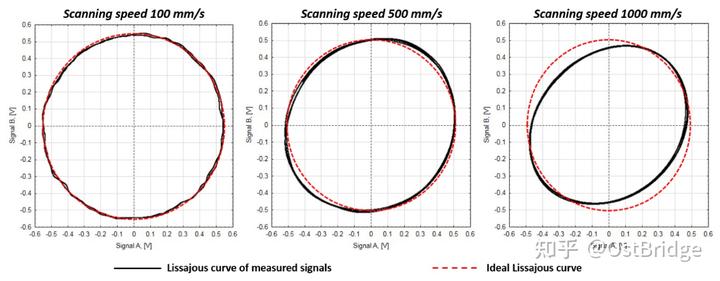
Zunächst überprüften wir die Leistung des Testlinien-Encoders bei verschiedenen Geschwindigkeiten. Der Encoder-Lieferant gab eine maximale Verfahrgeschwindigkeit von 100, 500 und 1000 mm/s an. Abbildung 5 zeigt die Lissajous-Kurven für mehrere Signalzyklen bei 100, 500 und 1000 mm/s.
Abbildung 5. Lissajous-Kurven für verschiedene Signalperioden bei Geschwindigkeiten von 100, 500 und 1000 Millimetern pro Sekunde.
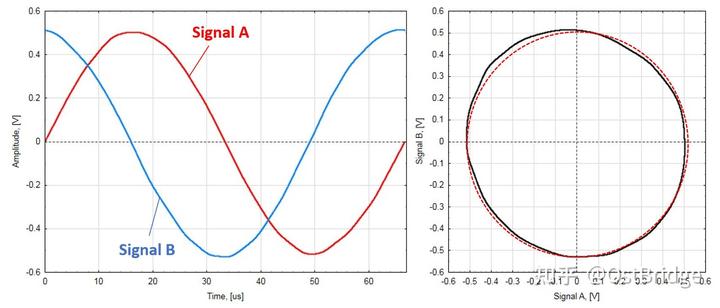
Aus diesen Diagrammen ist ersichtlich, dass die Leistung des Encoders nachlässt. Mit steigender Abtastgeschwindigkeit verändern sich Größe und Form der Lissajous-Kurve, und es tritt ein höherer SDE-Wert auf. Zur detaillierteren Untersuchung wurde der Lesekopf des Test-Encoders mit einer Geschwindigkeit von 100 mm/s im Bereich von 100 bis 1100 mm/s bewegt. Das elektrische Ausgangssignal wurde mit einer Abtastfrequenz von 250 MHz aufgezeichnet und der SDE-Wert gemäß der im vorherigen Abschnitt beschriebenen Methode bestimmt. Abbildung 6 zeigt beispielsweise die grafische Darstellung der elektronischen Signale und deren Kombination im XY-Diagramm bei einer Abtastgeschwindigkeit des Lesekopfs von 300 mm/s.
Abbildung 6. Elektronische Signale und deren Verhalten im XY-Diagramm. Der Encoder arbeitet mit einer seitlichen Geschwindigkeit von 300 Millimetern. Der bei dieser Geschwindigkeit berechnete mittlere SDE-Wert ist in Abbildung 7 dargestellt.
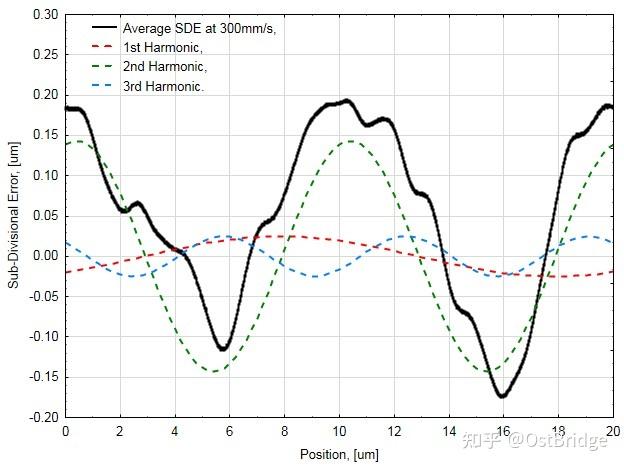
Die FFT-Analyse zeigt, dass die erste, zweite und dritte Harmonische den größten Einfluss auf die Fehleramplitude haben. Daher werden alle drei ersten Harmonischen im selben Diagramm dargestellt, um den Einfluss jeder einzelnen Harmonischen zu verdeutlichen. Die Gesamtfehleramplitude beträgt ± 0.185 µm. Die zweite Harmonische, die zweimal pro Zyklus auftritt, erzeugt den maximalen Fehlerwert.
Abbildung 7. Durchschnittliche SDE und ihre Zerlegung in drei erste Harmonische bei einer Dosengeschwindigkeit von 300 mm/s.
Die Datenverarbeitung erfolgte in der gleichen Geschwindigkeit wie bei allen Tests. Die berechnete Gesamtfehlermarge ist in Abbildung 8 grafisch dargestellt.
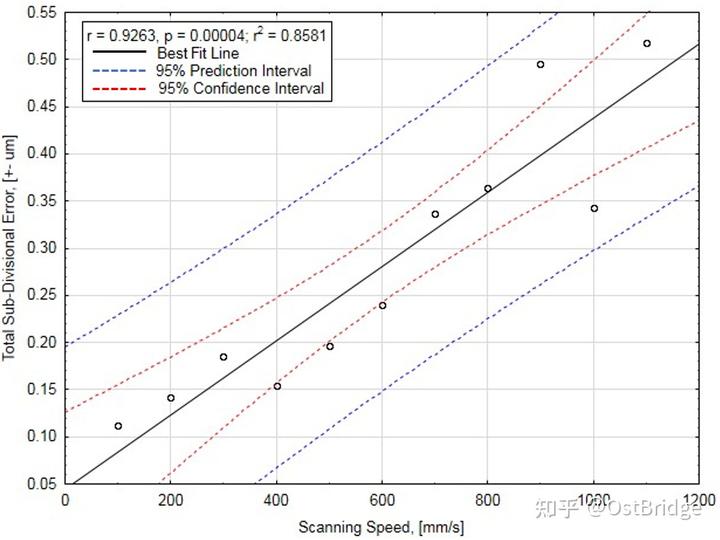
Die Ergebnisse zeigen einen starken linearen Zusammenhang zwischen Abtastgeschwindigkeit und Gesamtfehler. Mehr als 85 % des experimentell ermittelten Fehlers lassen sich mathematisch auf die kontinuierlich steigende Encodergeschwindigkeit zurückführen (R² = 0.8581). Der größte Fehler beträgt ± 0.52 µm bei 1100 mm/s, und es besteht ein signifikanter Unterschied im linearen Zusammenhang zwischen den Fehlern bei 900 mm/s und 1000 mm/s.
Abbildung 8. Abhängigkeit des gesamten SDE von der Scangeschwindigkeit. Datenpunkte und erster statistischer Parameter.
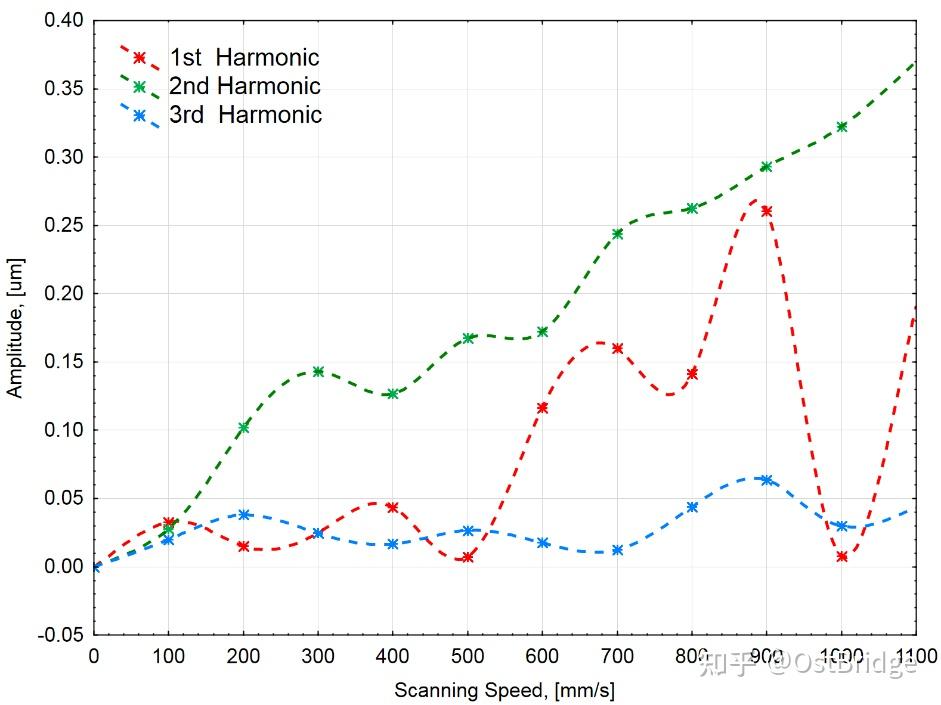
Um die physikalische Bedeutung der während des Abtastvorgangs auftretenden Fehler zu verstehen, analysierten wir die Größe und das Verhalten der ersten drei Fehlerharmonischen. Ihre Abhängigkeit von der Abtastgeschwindigkeit des Testencoders ist in Abbildung 9 dargestellt.
Abbildung 9. Die dritte Harmonische der ermittelten SDEs bei verschiedenen Geschwindigkeiten.
Der maximale Anteil des SDE bei jeder Geschwindigkeit wird durch die zweite Harmonische verursacht. Diese Harmonische zeigt einen starken linearen Zusammenhang mit der Durchgangsgeschwindigkeit (R² = 0.96). Ihre Amplitude nimmt proportional mit steigender Geschwindigkeit zu. Dieses Fehlerverhalten resultiert aus Amplitudenänderungen, Phasenverschiebungen oder einer Kombination aus beidem.
Die erste Harmonische des Fehlers zeigt einen nichtlinearen Zusammenhang. Der Amplitudenwert beginnt anzusteigen, sobald die Encodergeschwindigkeit 500 Millimeter pro Sekunde oder mehr erreicht. Im Bereich von 900 bis 1000 Millimeter pro Sekunde sind die extremen Wertsprünge zu beobachten. In diesem Bereich sinkt die Amplitude relativ von 0.26 Mikrometer auf 0.01 Mikrometer. Diese Harmonische entsteht durch eine horizontale Verschiebung des elektrischen Signals von Null.
Die Bedeutungsänderung der dritten Harmonischen ist im Vergleich zu den anderen nicht signifikant. Ihre Amplitude erreicht einen Maximalwert von 0.06 µm. Dieser Wert wurde, wie auch bei der ersten Harmonischen, bei einer Abtastgeschwindigkeit von 900 Millimetern pro Sekunde beobachtet. Üblicherweise entsteht diese dritte Harmonische durch Veränderungen während des optischen Abtastvorgangs.
Aus den erzielten Ergebnissen lassen sich folgende Schlussfolgerungen ziehen:
- Die erste Auswertung der Lissajous-Kurve zeigt, dass die SDE des getesteten Encoders von der Abtastgeschwindigkeit abhängt. Um einen Zusammenhang zu ermitteln, sind detailliertere Analysen bei verschiedenen Geschwindigkeiten erforderlich.
- Statistische Untersuchungen zeigen einen starken linearen Zusammenhang zwischen SDE und Abtastgeschwindigkeit. Daher ist es wichtig, die maximale Bewegungsgeschwindigkeit des Encoders in der jeweiligen Anwendung zu kennen. Unterschiedliche Maximalgeschwindigkeiten führen zu unterschiedlichen maximalen SDE-Werten und setzen klare Grenzen für die höchste Auflösung. Bleibt die Bedeutung von SDE über den gesamten Geschwindigkeitsbereich konstant oder ist der Zusammenhang nichtlinear, sollte der maximale SDE-Wert ermittelt werden.
- Die empfohlene maximale Betriebsgeschwindigkeit des Encoders beträgt 1 m/s. Innerhalb dieses Bereichs liegt die maximale Standardabweichung (SDE) bei ± 0.49 µm und erreicht bis zu 900 mm/s. Nach der Interpolation der Encodersignale sollte die Auflösung größer als 0.5 µm sein. Andernfalls ist der Interpolationsfehler größer als die Messschrittweite.
- Bei jeder Geschwindigkeit bildet der größte Teil des SDE-Budgets eine zweite Harmonische. Dies steht in direktem Zusammenhang mit der Geschwindigkeitserhöhung. Das bedeutet, dass die Differenz in der Signalamplitude oder Phasenverschiebung mit zunehmender Geschwindigkeit ansteigt. Amplituden- oder Phasenfehler können durch die physikalischen Prinzipien der optischen Abtastung, dynamisches Verhalten und fehlerhafte Justierung verursacht werden. Elektronische Bauteile (wie Fotodioden, verwendete Prozessoren oder Analogverstärker) sowie die Qualität und andere Einflüsse der verwendeten Kabel können ebenfalls eine Rolle spielen. Diese Aspekte müssen nicht nur im Entwicklungsprozess, sondern auch bei der Auswahl des geeigneten Encoders für spezifische Anwendungen berücksichtigt werden. Beispielsweise basiert das Funktionsprinzip des getesteten Encoders auf der Vierfeldabtastung. Erfordert die Anwendung eine höhere Stabilität der Abtastgeschwindigkeit oder erhöht sich die Wahrscheinlichkeit einer Skalenverunreinigung, muss ein optischer Encoder auf Basis der Einfeldabtastung gewählt werden.
- Die bei Geschwindigkeiten von 900 und 1000 Millimetern pro Sekunde berechneten Gesamt-SDE-Werte weichen von der ermittelten linearen Beziehung ab. Bei der Analyse der ersten Harmonischenkarte zeigen sich ab einer Geschwindigkeit von 500 mm/s deutliche Änderungen des Stellfehlers des Encodersignals. Der Lesekopf ist ein komplexes mechanisches Bauteil mit optischen und elektronischen Komponenten sowie einer Federaufhängung. Daher können selbst kleinste Verschiebungen, Abstandsänderungen, Neigungen oder relative Positionsänderungen zwischen dem Abtastgitter und dem Messsystem durch Resonanzfrequenzen, Reibung oder andere Kräfte hervorgerufen werden.
- Die FFT-Analyse zeigt, dass der Hauptteil der SDE nur aus wenigen ersten Harmonischen besteht. Dies bedeutet, dass sich der Verlauf der SDE mithilfe einer einfachen Gleichung, die lediglich Informationen über drei erste Harmonische (n=3) enthält, recht genau annähern lässt.
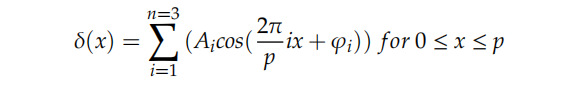
Nach weiterer Auswertung der experimentellen Messdaten lässt sich eine multivariate Funktion der SDE-Werte ermitteln. Diese Funktion liefert den ungefähren SDE-Wert der relativen Position innerhalb eines Zeitraums bei beliebiger Abtastgeschwindigkeit. Ebenso gibt sie den ungefähren SDE-Wert innerhalb eines Zyklus bei beliebiger Abtastgeschwindigkeit an.
Wobei f (x) eine multivariate Näherungsfunktion des SDE-Wertes ist, mit Parametern wie der relativen Position x und der Abtastgeschwindigkeit v.
ε steht für den zufälligen Fehler, und vMax steht für die maximale Geschwindigkeit des Encoders.
ε repräsentiert den zufälligen Fehler und vMax die maximale seitliche Geschwindigkeit des Encoders. Diese Gleichung kann zur Echtzeit-SDE-Kompensation verwendet werden.
5. Fazit
Lineare Encoder werden häufig zur präzisen Wegmessung beweglicher Einheiten eingesetzt, um Position und Geschwindigkeit zu steuern. Für die korrekte Ausführung dieser Aufgaben sind die Encoderparameter, wie Genauigkeit und Auflösung, entscheidend. In der Praxis ist der Standardfehler (SDE) optischer Encoder unvermeidbar. Die Größe dieses Fehlers begrenzt die maximale Auflösung und verursacht Geschwindigkeitsschwankungen. Es ist wichtig, die Grenzen des verwendeten Encoders zu verstehen, wenn Encodersignale für die Interpolation ohne Fehlerkorrektur- oder Kompensationsverfahren simuliert werden. Die in diesem Artikel beschriebene Methode dient der Bestimmung von Größe und Verlauf des Standardfehlers linearer Encoder. Gemäß der vorgeschlagenen Methode wurden experimentelle Untersuchungen am Standard-Linear-Gitter-SDE bei verschiedenen Abtastgeschwindigkeiten durchgeführt. Eine detaillierte Analyse des ermittelten Fehlers kann dessen physikalische Eigenschaften und die Grenzen des Encoders aufzeigen. Basierend auf den Ergebnissen lassen sich die Schwachstellen der Prüfausrüstung identifizieren und deren Leistung verbessern.
Die Kartierung und die approximative SDE bei verschiedenen Geschwindigkeiten können als multivariate Funktionen zur Kompensation von Positionsfehlern dienen. Dies ist unsere zukünftige Forschungsrichtung.